LA POUSSEE D'ARCHIMEDE
Définition: Principe d'archimède "Tout corps plongé dans un liquide (ou gaz) reçoit une poussée, qui s'exerce de bas en haut, et qui est égale au poids du volume de liquide déplacé."
La poussée d'Archimède est la force particulière que subit un corps plongé en tout ou en partie dans un fluide (liquide ou gaz) soumis à un champ de gravité.
Cette force provient de l'augmentation de la pression du fluide avec la profondeur (effet de la gravité sur le fluide, voir l'article hydrostatique) : la pression étant plus forte sur la partie inférieure d'un objet immergé que sur sa partie supérieure, il en résulte une poussée globalement verticale orientée vers le haut.
Cette poussée définit la flottabilité d'un corps
Définition: Principe d'archimède "Tout corps plongé dans un liquide (ou gaz) reçoit une poussée, qui s'exerce de bas en haut, et qui est égale au poids du volume de liquide déplacé."
La poussée d'Archimède est la force particulière que subit un corps plongé en tout ou en partie dans un fluide (liquide ou gaz) soumis à un champ de gravité.
Cette force provient de l'augmentation de la pression du fluide avec la profondeur (effet de la gravité sur le fluide, voir l'article hydrostatique) : la pression étant plus forte sur la partie inférieure d'un objet immergé que sur sa partie supérieure, il en résulte une poussée globalement verticale orientée vers le haut.
Cette poussée définit la flottabilité d'un corps
Histoire : le roi Hièron II de Syracuse demanda à Archimède de vérifier si la couronne était faite totalement en or ou si l’artisan y avait mis de l’argent. Archimède trouva le moyen desavoir si lacelle-ci était totalement en or , alors qu’il était au bain public , en observant comment les objets flottaient il serait alors sorti dans la rue en s’écriant « EURËKA » (j’ai trouvé).
Archimède constate que, pour un même volume donné, les corps n’ont pas le même poids apparent, c’est à dire une masse par unité de volume différente. On parle de nos jours de masse volumique.
La poussée d’Archimède est une force de pression répartie sur tout le volume du solide émergé.
En effet un corps flote lorsque : P(Poids)=A(Poussée d'archimede)
Exemple :
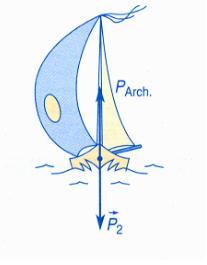
Cette force est caractérisée par :
- point d’application = centre d’inertie du solide immergé
- direction = verticale
- sens = vers le haut
- valeur = PA = ρfluide x Vsolide x g
Poussée d’Archimède f PA = ρfluide x Vsolide x g gintensité (N/kg)
(N) ↑ ↑
Masse volumique volume de fluide
du fluide ( kg /m3) déplacé (m3)
DE QUOI LA POUSSEE D'ARCHIMEDE DEPEND ELLE?
1) La profondeur ?
Schéma de l'expérience :
[Le corps utilisé est le même dans les deux situations]
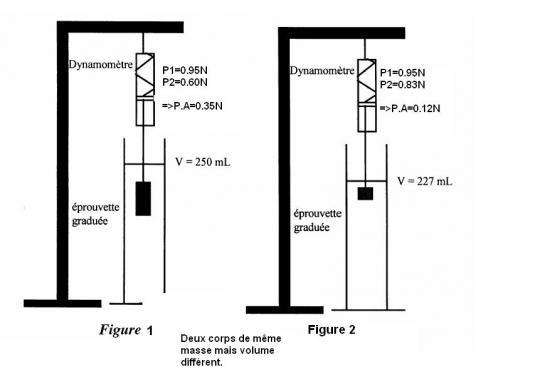
Conclusion : La poussée d'Archimede est plus importante sur la figure 1. Nous pouvons donc en conclure que le volume a une influence sur la poussée. En effet plus le corps immergé est volumineux, plus la poussée d'archimede sera grande
2) La nature du fluide?Schéma de l'expérience :
ρeau = 1,00 g/mL
ρalcool = 0.80 g/mL
[Le corps immergé est le même dans les deux situations]
ρeau = 1,00 g/mL
ρalcool = 0.80 g/mL
[Le corps immergé est le même dans les deux situations]
Conclusion: La poussée d'Archimede est plus importante lorsque le corps est immergé dans l'eau. On peut donc en conclure que la nature du fluide a une influence sur la poussée d'Archimede. En effet plus la densité du liquide est importante, plus la poussee d'archimede sera grande.
• La poussée d'Archimède varie donc en fonction du volume du corps immergé et de la masse volumique (ρ) du fluide.
UNE APPLICATION INTERESSANTE: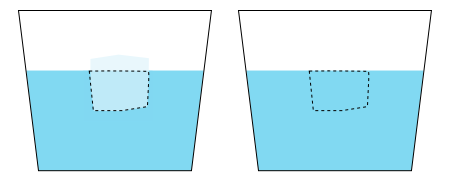
Un glaçon flotte dans un verre d'eau. Quel sera le niveau de l'eau lorsque ce glaçon sera totalement fondu? Aura t'il diminué, augmenté ou sera t'il inchangé?
La fonte d'un morceau de glace flottant sur de l'eau se produit sans changement de niveau de l'eau. En effet le volume de glace immergé correspond au volume d'eau liquide nécessaire pour égaler le poids du glaçon. En fondant, le glaçon produit (par conservation de la masse) exactement ce volume d'eau, qui « bouche le trou laissé par la disparition de la glace solide ». Le niveau d'eau reste le même. Sur la figure ci-contre, le volume délimité en pointillé est, dans le verre de gauche, le volume de glace immergée, et dans le verre de droite, le volume d'eau liquide produit par la fonte du glaçon.
On peut également faire le calcul suivant : si on considère, par exemple, un glaçon de 1 cm3 et de masse volumique 0,917 g·cm-3 (qui contient donc 0,917 g d'eau), le volume immergé sera de 0,917 cm3 (comme pour un iceberg, la majeure partie est sous l'eau). Lorsque le glaçon aura fondu, ces 0,917 g d'eau qui auront désormais une masse volumique de 1 g·cm-3 occuperont exactement le volume qu'occupait la partie immergée du glaçon.
• La poussée d'Archimède varie donc en fonction du volume du corps immergé et de la masse volumique (ρ) du fluide.
UNE APPLICATION INTERESSANTE:

Un glaçon flotte dans un verre d'eau. Quel sera le niveau de l'eau lorsque ce glaçon sera totalement fondu? Aura t'il diminué, augmenté ou sera t'il inchangé?
La fonte d'un morceau de glace flottant sur de l'eau se produit sans changement de niveau de l'eau. En effet le volume de glace immergé correspond au volume d'eau liquide nécessaire pour égaler le poids du glaçon. En fondant, le glaçon produit (par conservation de la masse) exactement ce volume d'eau, qui « bouche le trou laissé par la disparition de la glace solide ». Le niveau d'eau reste le même. Sur la figure ci-contre, le volume délimité en pointillé est, dans le verre de gauche, le volume de glace immergée, et dans le verre de droite, le volume d'eau liquide produit par la fonte du glaçon.
On peut également faire le calcul suivant : si on considère, par exemple, un glaçon de 1 cm3 et de masse volumique 0,917 g·cm-3 (qui contient donc 0,917 g d'eau), le volume immergé sera de 0,917 cm3 (comme pour un iceberg, la majeure partie est sous l'eau). Lorsque le glaçon aura fondu, ces 0,917 g d'eau qui auront désormais une masse volumique de 1 g·cm-3 occuperont exactement le volume qu'occupait la partie immergée du glaçon.
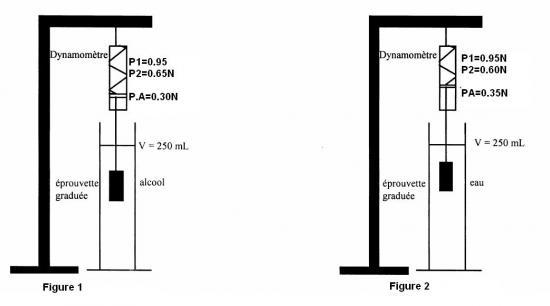
Les corps utilisés ont le même volume mais une masse différente.
Soit P1 le poids initial, P2 le poids apparent (poids du solide immergé) et PA : la poussée d'Archimede
Soit P1 le poids initial, P2 le poids apparent (poids du solide immergé) et PA : la poussée d'Archimede
Constat : Nous remarquons que la valeur de la poussée ne change pas. Nous pouvons donc en conclure que pour des corps de même volume, la poussée d'Archimede ne dépend pas de leur masse.
3) Le volume du solide immergé?
Schéma de l'expérience :
Les deux corps ont la même masse mais un volume différent. V1 > V2.
3) Le volume du solide immergé?
Schéma de l'expérience :
Les deux corps ont la même masse mais un volume différent. V1 > V2.
4) La masse?
Schéma de l'expérience :
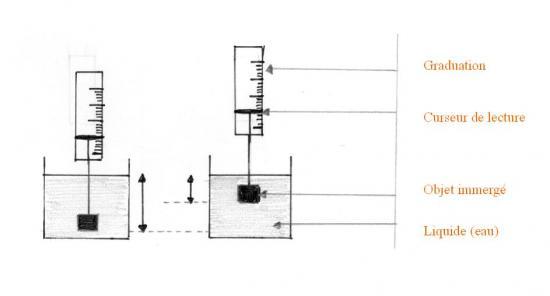
Constat : La poussée d'archimede ne varie pas en fonction de la profondeur. La profondeur n'a donc pas d'influence sur la poussée.


Merci beaucoup
RépondreSupprimer